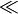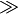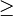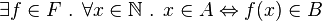A influência da matemática na música.

O que música tem a ver com matemática? Muito mais coisas do que podemos imaginar. As melodias que nos emocionam, são, na verdade, construídas a partir de relações matemáticas muito precisas. O engenheiro eletrônico Miguel Ratton, formado pela Universidade Federal do Rio de Janeiro (UFRJ), dá mais detalhes sobre como funciona a dobradinha fundamental música/matemática na entrevista abaixo, confira:

O engenheiro eletrônico Miguel Ratton
(Foto: Divulgação)

Qual a relação entre a música e a matemática? A música não existe sem a matemática?
A música já existia antes do desenvolvimento da matemática, porque a combinação dos sons, ainda que em boa parte dominada por relações matemáticas, baseia-se em nossa percepção psicoacústica, ou seja, nossa percepção fisiológica do som.

Então, a formação do som e da música é um processo físico?
Totalmente. O som é um fenômeno físico e como tal faz parte do estudo da física. A música é a arte da combinação de sons (e silêncios). Portanto, para entender profundamente música é necessário conhecer física.

Quais teorias matemáticas (teoria dos conjuntos, teoria dos números, álgebra abstrata...) podem ser aplicadas à música? De que forma e por quê?
A música pode ser usada para ilustrar alguns conceitos matemáticos. As figuras de tempo (duração) das notas, por exemplo, são frações de compasso do tipo 1/2, 1/4, 1/8, etc. A altura (afinação) das notas é estabelecida por uma relação exponencial, do tipo "2 elevado a x/12", onde x é a distância de uma nota a outra. A nossa percepção de intensidade dos sons se dá de forma exponencial e por isto medimos intensidade usando uma escala logarítmica (decibel). Já a teoria dos conjuntos poderia ser usada para distinguir alguns harmônicos (frequências múltiplas inteiras) de uma nota que também estão presentes em outra nota.

Os sons constituem o que se chama de escala musical, e eles são definidos de forma matemática, certo?
A escala musical usada atualmente pela maioria dos povos é a escala "igualmente temperada". Esta escala foi estabelecida por volta do século 17I e caracteriza-se por uma relação exponencial: a "distância" entre uma nota e sua oitava (o dobro da frequência) foi dividida exponencialmente em doze partes, de maneira que a relação entre qualquer nota e sua vizinha anterior (exemplo: dó# e dó) é sempre igual à raiz 12 de 2 (aproximadamente 1,059). O estabelecimento dessa escala não foi por acaso, mas sim para resolver o problema que havia nas escalas anteriores, que eram baseadas nas relações puras (3/2, 4/3, etc), definidas originalmente por Pitágoras, e que não permitiam a execução de qualquer música em qualquer tonalidade. A escala temperada possibilita que se façam transposições de tonalidade e modulações sem os inconvenientes (intervalos desafinados) das escalas antigas. É importante observar que, ao se ajustar a escala para o temperamento igual, as relações entre as notas da escala (exceto a oitava) deixaram de ser "acusticamente perfeitas" (3/2, 4/3, 5/4, etc). Esses erros, no entanto, são muito pequenos e não são percebidos pela maioria das pessoas.

Um som agradável ou desagradável tem a ver com a relação matemática entre os sons?
Certamente. Duas notas soando juntas são agradáveis ou não conforme a distância de suas alturas (frequências), sobretudo pela combinação de seus harmônicos. O intervalo mais consonante é a oitava, onde a frequência de uma nota é o dobro da outra e todos os seus harmônicos são iguais. Já no intervalo de quinta, metade dos harmônicos se combinam. A consonância tem a ver com as regiões do ouvido interno que são excitadas pelas duas notas e seus harmônicos: quando essas regiões estão muito próximas, a percepção individual de cada som é dificultada, causando uma sensação desagradável ("aspereza"). Esses intervalos podem ser definidos matematicamente.

Como se formam as notas musicais? Elas estão ligadas também à matemática? De que maneira?
Como mencionei anteriormente, as alturas das notas da escala são determinadas por relações matemáticas. As sete notas naturais (dó, ré, mi, fá, sol, lá, si) foram determinadas inicialmente a partir de relações fundamentais. Posteriormente, foram adicionadas as outras cinco notas ("acidentes" - sustenidos/bemóis) para completar os espaços entre todas as notas.

Existem registros na Antiguadade de estudos que relacionavam música e matemática?
O sábio grego Pitágoras provavelmente foi o maior estudioso da antiguidade sobre o assunto, e a escala que usamos hoje foi baseada na escala pitagórica. Mas também há indícios de que na antiga China já havia estudos de uma escala temperada.

Qual a diferença entre ritmo e harmonia?
Ritmo é a combinação de sons no decorrer do tempo. Harmonia é a combinação de sons simultâneos. Poderíamos dizer que o ritmo é "horizontal" e a harmonia é "vertical" - exatamente como representamos na pauta.

O ensino da música pode contribuir para o aprendizado da matemática? E também de outras matérias?
Acredito que a música possa ilustrar e tornar mais divertido o aprendizado de disciplina, como a matemática e a física. Muitas pessoas que gostam de matemática e física acabam se interessando pela música e vice-versa.

A importância da Matemática no nosso dia a dia!

Todos nós já fizemos ou já ouvimos perguntas do tipo:

“Porque esse monstro existe?”; “Para que serve a Matemática na minha vida?”;

“Porque eu preciso estudar Matemática?”;  Qual é a importância da Matemática na minha vida?”

São perguntas muito comuns  feitas por pessoas que não gostam do assunto ou que nem se deram conta de sua infinita importância em nosso cotidiano.
Como vou mostrar, ela aparece cada vez mais no nosso dia a dia, de forma muito intensa e simplesmente posso garantir que não vivemos sem ela.

Você  quer uma prova? Passe no mínimo uma hora do seu dia sem estar ligado ou  relacionado a números. Isso é impossível, pois estamos ligados a eles o tempo todo, desde o momento que acordamos. Temos que acordar com o despertador marcando um “número”, temos que calcular o tempo que levamos até chegar no trabalho, escola, etc.  e ai estão mais números!

Outro exemplo bem simples de ser enrolado é quando vamos a uma loja ou fazemos uma compra e o vendedor dá um desconto ou um acréscimo na compra. Se não soubermos como calculá-los vamos perdendo dinheiro  durante a nossa vida sem nos darmos conta.

Faça outro pequeno teste e veja quantas vezes a matemática aparece no seu dia a dia, seja no trabalho, seja em casa, seja na escola, curso ou faculdade, seja num clube ou shopping, num cinema, no computador, no diálogo com seu grupo de amigos.

Se ficarmos atentos a tudo que acontece ao nosso redor, iremos ver que a matemática não se trata apenas de uma simples diversão ou de uma simples aula chata na escola, mas sim, de um conteúdo bastante importante que faz parte de nossas vidas e que carregaremos pelo resto da vida!

Os melhores profissionais de todas as áreas, inclusive àquelas que não são afins, são exímios Matemáticos. Imagine você que trabalhando com Marketing digital sem saber calcular métricas de vendas, é o caminho mais rápido para o fracasso.

Tem pessoas que fazem a faculdade de Direito porque acham que não tem Matemática lá. Doce engano, pois o profissional do Direito utiliza a Matemática quando trabalha com causas que envolvam a realização de cálculos, como por exemplo bens, valores, partilhas e heranças. E se ele for tributarista então vai se ver envolvido com cálculos a vida toda. Não se engane pois em todas as profissões a Matemática está presente.

Até uma simples dona de casa usa medidores de massa (kg) em sua cozinha para fazer suas receitas. Ela nem sabe mas está sempre conectada com a Matemática.

Chegou o momento em que a humanidade percebeu que não dá pra viver sem os conhecimentos matemáticos, ou seja, a Matemática desempenha um papel de fundamental importância nos âmbitos da sociedade, desde uma simples compra de um produto, até as mais complexas situações cotidianas.

Da mesma forma que fórmulas, equações teorias e teoremas que estudamos na escola é Matemática, qualquer pensamento artístico, religioso, social, psicológico, são processos mentais matemáticos que nos acompanham desde que nascemos.

Portanto, não se iluda, no universo tudo tem base na Matemática, desde o pensamento as artes,danças Ciências , a natureza e a vida!

matemática e seus símbolos

símbolo em HTML	símbolo em TEX	Nome	Definição	Aplicação
		Lido como
		Conceito
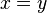=		Igualdade é igual a; igual qualquer operação	significa  e  representam a mesma coisaou o mesmo valor  e  são nomes diferentes para a exata mesma coisa.
≠		Inequação não é igual a; não iguala qualquer operação	significa que  e  não representam a mesma coisa ou o mesmo valor. (As formas !=, /= ou <> são geralmente usadas em programação onde facilita a digitação e são preferidas no uso do ASCII.)
< >		Desigualdade é menor que, é maior do que Teoria da ordem	significa que  é menor que .  significa que  é maior que .
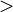
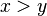		subgrupo apropriado é um subgrupo adequado de Teoria dos grupos	significa que  é um subgrupo adequado de . (Um subgrupo apropriado de um grupo G é um subgrupo H, que é um subconjunto apropriado de G (isto é, ).)
≪ ≫		enormeDesigualdade estrita é muito menor que, é muito maior que Teoria da ordem	x ≪ y significa que x é muito menor que y. x ≫ y significa que x é muito maior que y.	0.0001 ≪ 1000000
		Comparação assintótica é de uma ordem inferior a, é de uma ordem superior a 4,2 Teoria analítica dos números	f ≪ g significa que o crescimento de f é assintoticamente delimitado por g. (Esta é a notação de I M Vinogradov. Outra anotação é a notação assintótica do Big O, que se parece comf = O(g).)	x ≪ ex
≤ ≥		Desigualdade é menor ou igual a, é maior ou igual a Teoria da ordem	x ≤ y significa que x é menor ou igual a y. x ≥ y significa que x é maior ou igual a y. (As formas "<=" e ">=" são geralmente utilizado em linguagens de programação, onde a facilidade de uso e de digitação de texto ASCII é preferido.)	3 ≤ 4 e 5 ≤ 5 5 ≥ 4 e 5 ≥ 5
		Subgrupo é um subgrupo de Teoria dos grupos	H ≤ G significa que H é um subgrupo de G.	Z ≤ Z A3  ≤ S3
		Redução é redutível a Complexidade computacional	A ≤ B signifa que o problema A pode ser reduzido para o problema B. ( Subscritos podem ser adicionados à ≤ para indicar qual tipo de redução.)	Se então
		≦ ≧		Relação de congruência ...é inferior a ... é maior do que... Aritmética modular	7k ≡ 28 (mod 2) só é verdadeiro se k é um inteiro par. Suponha que o problema requer k ser não-negativo, o domínio é definido como 0 ≦ k ≦ ∞.	10a ≡ 5 (mod 5)    para 1 ≦a ≦ 10

Símbolo	Nome	lê-se como	Categoria
+	Adição	Mais	Aritmética
	4 + 6 = 10 significa que se se somar 4 a 6, a soma, ou resultado, é 10.
	Exemplo: 43 + 65 = 108; 2 + 7 = 9
-	Subtração	Menos	Aritmética
	9 - 4 = 5 significa que se se subtrair 4 de 9, o resultado será 5. O sinal - é único porque também denota que um número é negativo. Por exemplo, 5 + (-3) = 2 significa que se se somar cinco e menos três, o resultado será dois.
	Exemplo: 87 - 36 = 51
÷ ⁄	Divisão	Dividir	Aritmética
	6 ÷ 3 = 2 ou 6 ⁄ 3 = 2 significa que se se devidir 6 por 3, o resultado é 2.
	Exemplo: 100 ÷ 2 = 50
⇒ →	Implicação Material	Implica; se ... então	lógica proposicional
	A ⇒ B significa: se A for verdadeiro então B é também verdadeiro; se A for falso então nada é dito sobre B. → pode ter o mesmo significado de ⇒, ou pode ter o significado que mencionamos mais abaixo sobre as funções
	x = 2  ⇒  x² = 4 é verdadeiro, mas x² = 4   ⇒  x = 2 é em geral falso (visto que x pode ser −2)
⇔ ↔	equivalência material	se e só se; sse	lógica proposicional
	A ⇔ B significa: A é verdadeiro se B for verdadeiro e A é falso se B é falso
	x + 5 = y + 2  ⇔  x + 3 = y
∧	conjunção lógica	e	lógica proposicional
	a proposição A ∧ B é verdadeira se A e B foram ambos verdadeiros; caso contrário, é falsa
	Exemplo: n < 4  ∧  n > 2  ⇔  n = 3 quando n é um número natural
∨	disjunção lógica	ou	lógica proposicional
	a proposição A ∨ B é verdadeira se A ou B (ou ambos) forem verdadeiros; se ambos forem falsos, a proposição é falsa
	Exemplo: n ≥ 4  ∨  n ≤ 2  ⇔ n ≠ 3 quando n é um número natural
¬ ~	negação lógica	não	lógica proposicional
	a proposição ¬A é verdadeira se e só se A for falso Uma barra colocada sobre outro operador tem o mesmo significado que "¬" colocado à sua frente
	Exemplo: ¬(A ∧ B) ⇔ (¬A) ∨ (¬B); x ∉ S  ⇔  ¬(x ∈ S)
∀	quantificação universal	para todos; para qualquer; para cada	lógica predicativa
	∀ x: P(x) significa: P(x) é verdadeiro para todos os x
	Exemplo: ∀ n ∈ N: n² ≥ n
∃	quantificação existencial	existe	lógica predicativa
	∃ x: P(x) significa: existe pelo menos um x tal que P(x) é verdadeiro
	Exemplo: ∃ n ∈ N: n + 5 = 2n
=	igualdade	igual a	todas
	x = y significa: x e y são nomes diferentes para a exata mesma coisa
	Exemplo: 1 + 2 = 6 +3
: :⇔	definição	é definido como	todas
	x := y significa: x é definido como outro nome para y P :⇔ Q significa: P é definido como logicamente equivalente a Q
	Exemplo: cosh x := (1/2)(exp x + exp (−x)); A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B)
{ , }	chavetas de conjunto	o conjunto de ...	teoria de conjuntos
	{a,b,c} significa: o conjunto que consiste de a, b, e c
	Exemplo: N = {0,1,3....}
{ : } { | }	notação de construção de conjuntos	o conjunto de ... tal que ...	teoria de conjuntos
	{x : P(x)} significa: o conjunto de todos os x, para os quais P(x) é verdadeiro. {x | P(x)} é o mesmo que {x : P(x)}.
	Exemplo: {n ∈ N : n² < 20} = {0,1,2,3,4}
∅ {}	conjunto nulo	conjunto vazio	teoria de conjuntos
	{} significa: o conjunto sem elementos; ∅ é a mesma coisa
	Exemplo: {n ∈ N : 1 < n² < 4} = {}
∈ ∉	pertença a conjunto	em; está em; é um elemento de; é um membro de; pertence a ; existe em ,	teoria de conjuntos
	a ∈ S significa: a é um elemento do conjunto S; a ∉ S significa: a não é um elemento de S
	Exemplo: (1/2)−1 ∈ N; 2−1 ∉ N
⊆ ⊂	subconjunto	é um subconjunto [próprio] de	teoria de conjuntos
	Exemplo: A ⊆ B significa: cada elemento de A é também elemento de B (A é um subconjunto de B) A ⊂ B significa: A ⊆ B mas A ≠ B (A é um subconjunto próprio de B)
	Exemplo: A ∩ B ⊆ A; Q ⊂ R
∪	união teórica de conjuntos	a união de ... com ...; união	teoria de conjuntos
	A ∪ B significa: o conjunto que contém todos os elementos de A e também todos os de B, mas mais nenhuns
	Exemplo: A ⊆ B  ⇔  A ∪ B = B
∩	intersecção teórica de conjuntos	intersecta com; intersecta	teoria de conjuntos
	A ∩ B significa: o conjunto que contém todos os elementos que A e B têm em comum
	Exemplo: {x ∈ R : x² = 1} ∩ N = {1}
\	complemento teórico de conjuntos	menos; sem; excepto	teoria de conjuntos
	A \ B significa: o conjunto que contém todos os elementos de A que não estão em B
	Exemplo: {1,2,3,4} \ {3,4,5,6} = {1,2}
( ) [ ] { }	aplicação de função; agrupamento	de	teoria de conjuntos
	para a aplicação de função: f(x) significa: o valor da função f no elemento x para o agrupamento: execute primeiro as operações dentro dos parênteses
	Exemplo: Se f(x) := x², então f(3) = 3² = 9; (8/4)/2 = 2/2 = 1, mas 8/(4/2) = 8/2 = 4
f:X→Y	seta de função	de ... para	funções
	f: X → Y significa: a função f mapeia o conjunto X no conjunto Y
	Exemplo: Considere a função f: Z → N definida por f(x) = x²
N	números naturais	N	números
	N significa: {1,2,3,...}
	Exemplo: {|a| : a ∈ Z} = N
Z	números inteiros	Z	números
	Z significa: {...,−3,−2,−1,0,1,2,3,...}
	Exemplo: {a : |a| ∈ N} = Z
Q	números racionais	Q	números
	Q significa: {p/q : p,q ∈ Z, q ≠ 0}
	3.14 ∈ Q; π ∉ Q
R	números reais	R	números
	R significa: {limn→∞ an : ∀ n ∈ N: an ∈ Q, o limite existe}
	π ∈ R; √(−1) ∉ R
C	números complexos	C	números
	C significa: {a + bi : a,b ∈ R, b  ≠ 0}
	i = √(−1) ∈ C
< >	comparação	é menor que, é maior que	ordenações parciais
	x < y significa: x é menor que y; x > y significa: x é maior que y
	Exemplo: x < y  ⇔  y > x
≤ ≥	comparação	é menor ou igual a, é maior ou igual a	ordenações parciais
	x ≤ y significa: x é menor que ou igual a y; x ≥ y significa: x é maior que ou igual a y
	Exemplo: x ≥ 1  ⇒  x² ≥ x
√	raiz quadrada	a raiz quadrada principal de; raiz quadrada	números reais
	√x significa: o número positivo, cujo quadrado é x
	Exemplo: √(x²) = |x|
∞	infinito	infinito	números
	∞ é um elemento da linha numérica estendida que é maior que qualquer número real; ocorre com frequência em limites
	Exemplo: limx→0 1/|x| = ∞
π	pi	pi	geometria euclidiana
	π significa: a razão entre a circunferência de um círculo e o seu diâmetro
	Exemplo: A = πr² é a área de um círculo de raio r
!	factorial	factorial	análise combinatória
	n! é o produto 1×2×...×n
	Exemplo: 4! = 24
| |	valor absoluto	valor absoluto de; módulo de	números
	|x| significa: a distância no eixo dos reais (ou no plano complexo) entre x e zero
	Exemplo: |''a'' + ''bi''| = √(a² + b²)
|| ||	norma	norma de; comprimento de	análise funcional
	||x|| é a norma do elemento x de um espaço vectorial
	Exemplo: ||''x''+''y''|| ≤ ||''x''|| + ||''y''||
∑	soma	soma em ... de ... até ... de	aritmética
	∑k=1n ak significa: a1 + a2 + ... + an
	Exemplo: ∑k=14 k² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30
∏	produto	produto em ... de ... até ... de	aritmética
	∏k=1n ak significa: a1a2···an
	Exemplo: ∏k=14 (k + 2) = (1  + 2)(2 + 2)(3 + 2)(4 + 2) = 3 × 4 × 5 × 6 = 360
∫	integração	integral de ... até ... de ... em função de	cálculo
	∫ab f(x) dx significa: a área entre o eixo dos x e o gráfico da função f entre x = a e x = b
	∫0b x² dx = b³/3; ∫x² dx = x³/3
f '	derivada	derivada de f; primitiva de f	cálculo
	f '(x) é a derivada da função f no ponto x, i.e. o declive da tangente nesse ponto
	exemplo: Se f(x) = x², então f '(x) = 2x
∇	gradiente	del, nabla, gradiente de	cálculo
	∇f (x1, …, xn) é o vector das derivadas parciais (df / dx1, …, df / dxn)
	Exemplo: Se f (x,y,z) = 3xy + z² então ∇f = (3y, 3x, 2z)

Biologia e matemática, aplicadas e combinadas

Aproximação entre as duas áreas pode dar origem a novos campos. Tendência foi apresentada por matemático norte-americano em palestras que comemoram os 60 anos do Impa.

Por: Marcelo Garcia

Matemáticos preocupados com a estrutura de proteínas e biólogos com a análise dos ângulos formados entre seus aminoácidos. Talvez pareça estranho, mas a aproximação entre matemática e biologia tem se tornado mais comum nas últimas décadas e pode até mesmo dar origem a novos ramos da ciência. Em um ciclo de palestras realizado no contexto da comemoração dos 60 anos do Instituto de Matemática Pura e Aplicada (Impa), o premiado matemático norte-americano Stephen Smale, da Universidade da Califórnia, nos Estados Unidos, abordou o trabalho de seu grupo e as diversas possibilidades que surgem a partir dessa interação.

As possibilidades passam pelo entendimento dos mecanismos de dobras das proteínas. Se descobrirmos esse segredo, vamos responder a uma das questões mais fundamentais da biologia

Na ocasião, Smale apresentou os fundamentos matemáticos dessa nova abordagem e seu potencial para o estudo das estruturas moleculares e das formas de interação entre algumas moléculas básicas para a vida, como os peptídeos. “As possibilidades são muitas, como o aprimoramento de vacinas e o entendimento dos mecanismos por trás das dobras e do enovelamento das proteínas”, avalia. “Se descobrirmos esse segredo, vamos responder a uma das questões mais fundamentais da biologia.”

O matemático Marcelo Viana, coordenador de atividades científicas do Impa, lembra que uma das principais inspirações da matemática sempre foi a resolução dos problemas colocados pelas ciências experimentais. “Há algumas décadas, com os avanços na genética e na bioinformática, a biologia já vem obtendo bons resultados com a matemática tradicional em áreas como a epidemiologia e a dinâmica evolutiva”, explicou. “O trabalho de grupos como o de Smale, no entanto, busca mais; procura elaborar fundamentos matemáticos inovadores para as novas questões experimentais.”  

Viana compara os esforços desses matemáticos aos de cientistas como Isaac Newton eGottfried Leibniz, fundamentais para o desenvolvimento do cálculo infinitesimal há quase 400 anos. “Um dos principais motivadores do desenvolvimento do cálculo foi a necessidade de lidar com questões experimentais relacionadas ao estudo da astronomia”, avaliou. “Hoje os problemas e desafios apresentados pela biologia podem estimular uma nova visão da matemática, que também poderá beneficiar outras áreas.”

60 anos de aplicação

Um dos centros de matemática mais reconhecidos do mundo, com uma produção científica de grande qualidade, o Impa foi a primeira instituição brasileira criada pelo então Conselho Nacional de Pesquisas (CNPq), em 15 de outubro de 1952. De lá para cá, tornou-se centro de excelência para o pós-doutorado na avaliação da Academia de Ciências para o Mundo em Desenvolvimento (TWAS) e buscou estimular a pesquisa científica na área e difundir o aprimoramento da cultura matemática no país.

Viana: “Um dos nossos objetivos é combater a percepção pública da matemática como uma ciência difícil, abstrata e inacessível”

“O modelo do Impa serviu de inspiração para dezenas de outras instituições de matemática do país e o instituto funciona como um grande garoto propaganda da qualidade da matemática brasileira no mundo”, diz Viana. “Durante esse tempo, também formamos muitos matemáticos brasileiros e estrangeiros, especialmente da América Latina, que hoje atuam como embaixadores da matemática pelo continente.”

O Impa também se destaca por suas iniciativas de ensino e divulgação da matemática como a Olimpíada Brasileira de Matemática das Escolas Públicas e os colóquios brasileiros de matemática. “Um dos nossos objetivos é combater a percepção pública da matemática como uma ciência difícil, abstrata e inacessível”, defende Viana. “Para mudar essa imagem, muito propagada pela mídia, é preciso atuar na divulgação e estimular os pesquisadores a apresentar a área de forma mais concreta, mais relacionada ao mundo que nos rodeia.”